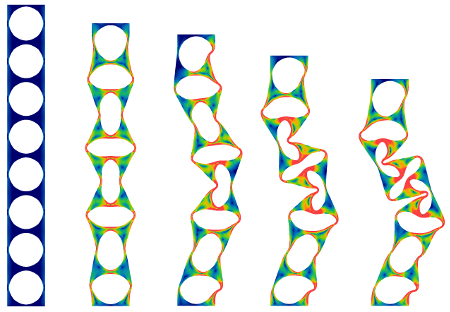Chris Johnson
Research
My UKRI-funded research projects are on Gateway to Research.
Granular segregation in geophysical flows
Rapid natural flows of granular material (such as debris flows, rock avalanches and lahars) frequently contain particles of a very wide range of sizes. Granular segregation contributes to a heterogeneous distribution of particles within the flow, which consequently alters the flow dynamics.
In Johnson et al. (2012) we studied the process of granular segregation in large-scale (~100m long) debris-flow experiments by combining measurements of the flow velocity field, the (spatially-varying) particle size distribution within the deposit, and the trajectories of marked tracer particles that were incorporated into the flow. We explained how particle size segregation and the velocity field at the front of a propagating debris flow combine to produce coarse, stationary levees, which channelise subsequent flow. This work was in collaboration with Dick Iverson and colleagues at the US Geological Survey. In Edwards et al. (2023), we modelled the three-dimensional segregation that takes place inside this flow mathematically, providing further insight into the structure and formation of the levees.



These coarse levees closely related to finger-like morphology observed in pyroclastic flow deposits. In Woodhouse et al. (2012) we develop a coupled model for the segregation and flow of a bidisperse mixture of grains, and find that numerical solutions exhibit fingered structures very similar to those observed in nature. A stability analysis of the model evinces the origin of these structures, and indicates that the wavelength of the instability is governed by terms that are commonly omitted in depth-averaged models. A viscosity obtained through the depth-averaging of the rheology provides a mechanism for this regularisation (Baker et al. 2016), also sets the unique width established by a levee-channelised granular flow (Rocha et al., 2019).
Wave formation in geophysical flows
Debris flows, snow avalanches and similar flows frequently form surge waves. These are often closely linked to segregation, with larger grains collecting at the front of each wave. In Viroulet et al. (2018) we explain how the interaction between waves and segregation in dry granular flows results in concentration of large grains at the wave crests. In Meng et al. (2022) we formulated a two phase grain-water model to explain the formation of the dry bouldery region frequently observed at the front of debris flows.
As of 2023, I am Co-I on two NERC projects looking at the behaviour of such waves in debris flows and snow avalanches.
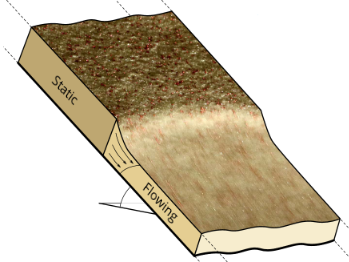
Depth-integrated descriptions of granular frictional hysteresis
An important aspect of many granular avalanches is the simultaneous presence of static and flowing granular material, with an interface between these at which grains are eroded or deposited. A subtle balance of forces determines the location and evolution of this interface, and thus the rate of erosion or deposition.
In depth-integrated models, the static and flowing states arise from a hysteretic description of the effective basal friction, with the interface between static and flowing grains corresponding to a non-equilibrium 'snap-through' transition between these states. We examine this process in detail by studying leveed channels (Rocha et al., 2019), the deposit left behind by a granular avalanche (Edwards et al., 2019), and the retrogressive erosion of a static granular layer (Russell et al., 2019). In the latter two cases the 'snap-through' is regulated by inertia, but in the case of a leveed channel the problem is steady, and the regularisation arises through lateral stresses. These are small and are almost always neglected in depth-integrated models, but here the lateral stresses are a singular perturbation and provide the physics that controls the channel width despite their small magnitude.
By examining situations in which the macroscopic flow behaviour is sensitive to the behaviour of the static/flowing interface, we are able to infer detailed information about the granular friction in the hysteretic (velocity-decreasing) region, which has not previously been possible.
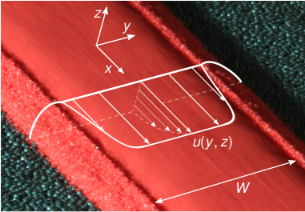
Gravity currents and intrusions
Gravity currents and intrusions are predominantly horizontal spreading flows driven by a difference in density (or in density gradient) between the current and the surrounding fluid. They occur frequently and at very large scales in the atmosphere and oceans. My work focuses on the construction and solution of depth-integrated models for these high Reynolds-number flows.
In Johnson & Hogg (2013) we derive a depth-integrated model for gravity currents that includes the effects of entrainment of ambient fluid into the currents. The entrained fluid not only dilutes the current, but also alters the dynamics, resulting in new asymptotic solutions for the flow at late times.
In Johnson et al. (2015) we investigate the spreading behaviour of volcanic ash clouds, modelled as intrusions that are fed by a continuous flux from a point source. We find solutions for both axisymmetric and wind-blown plumes, and couple these to a model for the distribution of ash within the plume. These show, contrary to previous assumptions, that flows in the absence of wind are non-self-similar, implying that simple scaling arguments and “box models” lead to incorrect deductions. In Pouget et al. (2016) we find good agreement between this model and observations of volcanic plumes, and additionally show how our model predicts the time-dependent establishment of the umbrella cloud, and the continued evolution of the cloud after the eruption ceases.
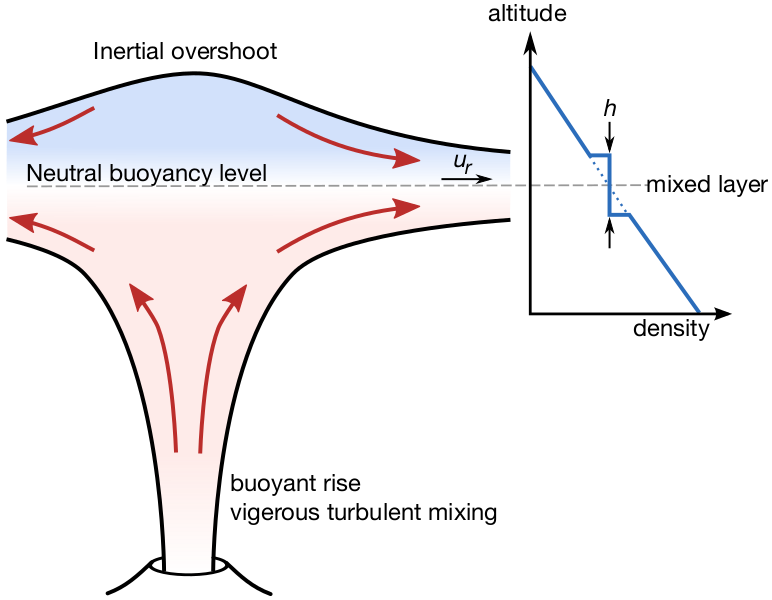

Motivated by the failure of box models in this context, in Ungarish et al. (2015) we develop a simple hybrid model (a development of the box model idea) for axisymmetric, continuously-supplied intrusions, and extend this to gravity currents, particle-driven flows, and (in Ungarish et al., 2016) rotating systems.
My collaborators on this work include Andrew Hogg, Marius Ungarish, Herbert Huppert, Steve Sparks, Jeremy Phillips and Marcus Bursik.
I am a Co-I on the V-PLUS project, a NERC highlight topic grant led by Anja Schmidt, Tamsin Mather and Mike Burton, which aims to combine volcanic plume modelling of the sort described above with satellite and ground-based measurements of ash and SO2, to provide an improved description of the dispersal of these throughout the atmosphere.
Bifurcations in perforated solids
A solid elastic column buckles sideways when compressed along its length, at a critical load shown by Euler to scale as one over the column length squared. In Johnson et al. (2017) we show that perforating the column with holes can cause this critical load to become independent of the column length, and dependent only on the geometry of the holes. We show also how this sideways buckling mode interacts with a second buckling mode, in which the holey column remains straight as it collapses, but the holes buckle alternately horizontally and vertically. The insight into this behaviour is obtained through bifurcation-tracking finite-element numerics and an asymptotic theory, which are also applied to the buckling of a two-dimensional perforated sheet.
In Box et al. (2020) we show how this behaviour is also observed in perforated columns and sheets of hard 'real-world' materials such as metals and plastics. In these materials, both elastic and plastic deformation play a role in the buckling, which makes the resulting deformations much more complex than the hyperelastic case. Nonetheless, the geometry of the holey column still allows the global compression and buckling behaviour of the objects to be inferred from their microstructure.