Research themes
We focus the vast expertise in our Department around key themes that maximize our ability to provide mathematical solutions to global societal issues.
Using the latest theories and applying up to date mathematical testing methods, we ensure we are assisting today's key challenges in areas such as health, engineering, finance and the physical world.

Algebra, logic and
number theory
We work across broad areas of fundamental pure research underpinning much of mathematics.

Analysis, geometry and dynamical systems
Our researchers describe properties of geometric structures and develop the theory and applications of dynamical systems.
Continuum mechanics
We work at the interface of theory, computation and experimentation with the aim of understanding an array of complex continua.

Mathematics in the life sciences
Our mathematicians work closely with life scientists to address key challenges in biology and medicine.
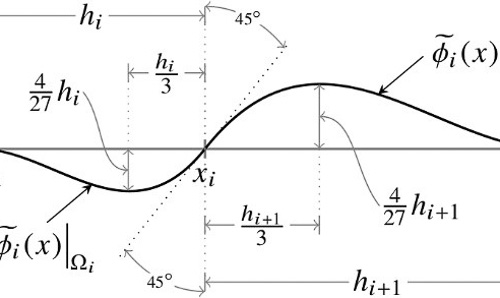
Numerical analysis and scientific computing
We develop and analyse algorithms that compute numerical approximations and apply them to real-world problems.
Probability, financial mathematics and actuarial science
Our research covers a wide range of topics in the field of probability and its application areas.